Welcome to my article on physics of the fish tank. I should start out saying that you could easily keep fish with out actually knowing any of this. It is however, in my opinion, interesting and of some value in understanding some of the aspects of aquaria. I have included some examples for tank sizes of 10,29, and 55 gallons, since they seem to be the most common. If you don’t have a tank that size you have to do the calculations you’re self. Sorry. Here is my rough table of contents:
1. Volume
2. Weight
3. Pressure
4. Stress on glass
5. Buoyancy
6. More about pressure, including gravel vac’s and pythons.
7. A little bit about electricity. (power usage and cost calculations)
8. How fast the tank cools.
9. More than you ever wanted to know about light
10. Those whacky refracting fishies
Ok, enough of that, time for the relevant stuff.
1.
Just how much water is in my tank?
This question is asked a lot, so here it is.
For a rectangle tank, you need to measure the length (L), width (W) and height (H) of the tank, then multiply them together. Volume (V)=LxWxH
Here are some examples for common tanks.
10 gallon:
L= 20 in V=20x10x12
W= 10 in V=2400 cu.in.
H= 12 in
29 gallon:
L=30 in V=30x12x18
W=12 in V=6480 cu.in
H= 18 in
55 gallon:
L=48 V= 48x13x20
W=13 V=12480 cu.in.
H=20
For some other odd shaped tanks:
Hex (all sides same length):
Find the length of a side (L)
Find the distance from the center of one flat side, to the opposite flat side (W).
Find the height of the tank (H).
V = 3xLxWxH
Cylinder:
Find the distance across the tank and divide by 2 (R).
Find the height of the tank (H).
V= 3.14 x R^2 x H (Note: R^2=R squared, or RxR)
Bow fronts can be difficult to measure. If the bow is perfectly circular or parabolic then it maybe possible to calculate the volume, but it is a lot of work and more easily done in different coordinates. I don’t want to get into that since I said that I would keep the math on the easier side.
For volume in gallons you multiply the volume in cubic what ever (inches in the examples) by a water volume constant (B). For inches B= .0043 For feet B = 7.5, thus, gallons=VxB
Examples:
10 gallons:
G= 2400x .0043= 10.3 gal
29 gallons:
G= 6480x .0043=27.9 gal
55 gallons:
G=12480x .0043= 53.7 gal.
As you can see, the advertised volumes are not the actual volumes of the tanks.
2.
Weight:
Calculating the actual weight of the aquarium can be quite difficult. You need the weight of the empty tank, all the decorations and gravel in the tank, and the amount of water in the tank. Water weighs 8.5 lbs per gallon, so for the average tank, you can assume about 10-12 lbs per gallons depending on what you have in it. Simply multiply the volume of the tank in gallons by 10 (in these examples) to get an approximate weight.
10 gallons:
W= 10x10 =100 lbs
29 gallons:
W= 29x10 = 290 lbs
55 gallons:
W = 55x10 = 550 lbs
As you can see, some tanks can get very heavy very fast. The 55 gallon weighs over a quarter of a ton!
3.
Oh the pressure!!! Just what is the water pressure down there? Just how deep can your air pump or CO2 go?
Well, pressure basically the weight of all the air in the atmosphere air and the weight of the water per one unit of area, usually per square inch. Normal atmospheric pressure is 14.7 pounds per square inch (psi). This means that if you draw a square on the ground one inch on each side, all of the air above it, from the ground to the edge of the atmosphere way up there weighs 14.7 lbs. Most measurements of pressure are relative to this. If your pump is rated at 1 psi, it is putting out 15.7 psi, but because the back pressure is 14.7, the net effect is 1 psi. All of our measurements are going to be relative to the atmospheric pressure.
Water pressure depends only on depth. To find it is simple, just multiply the density of water times its depth. The density of water (d) is .036 pounds per cubic inch (at sea level).
P= dxh
Examples:
10 gallons:
P= .036x 12 = .43 psi
29 gallons:
P= .036x 18 = .65 psi
55 gallons:
P= .036x 20= .72 psi.
If you have a small air pump rated at 1 psi, then it will just barely work in a 55 gallon tank, and its effective pressure out is only about .28 psi.
4.
Speaking of pressure, how strong is that silicone anyway?
Here is one place that things start to get a little more tricky, as this requires calculus. (OH NOW HIT THE BACK BUTTON NOW!!!!) No, no, no, don’t worry, its ok, you don’t need the calculus to figure it out in your tank, it’s just required to find the equation.
One think you need to know about pressure is that it works in “pushes” in every direction equally, so if the pressure is 10 psi, that means that on the sides of the tank, there are 10 psi.
To find the force on the side of the tank you simply need to multiply the area of the glass by the pressure. But wait, its not that simple, the pressure changes with depth. This is why the calculus is needed. If you under stand it, its included in the next paragraph. If not, then just ignore it and use the equation in the last line.
Note: I cannot make an integral sign, so I’ll use int(..) instead.
F = int( dxWxh dh) dh refers to the variable being integrated with respect to, basically.
F = ½ xdxWxh^2
To find the force on the side of the tank, just plug the numbers into the above formula.
Example (front or back walls):
10 gallons:
F= ½ x .036x20x12^2
F= 52 lbs.
29 gallons:
F= ½ x.036x30x18^2
F=175 lbs.
55 gallons:
F= ½ x.036x48x20^2
F= 346 lbs.
As you can see, there is a lot of force on the sides of a tank. Kind of makes you want to ensure your center brace is there huh? Notices that if you add up the forces on the front, back and side walls, it is more than the weight of the tank!!!
5.
While we are still on the topic of water, lets talk about water displacement. I remember a post once where someone asked if, since water displaces the weight of an object, does that mean that rocks weigh less? Well, the short answer is no.
Archimedes principle states that an object displaces its weight in water if it is floating (and only floating). Basically if something that is 10 lbs is floating, then it displaces 10 lbs of water. The volume of the water displaced is the same volume of the amount of the object under water. That is why ice is mostly under water when it floats (its just slightly lighter than water). When an object doesn’t float, its weight is being supported by the bottom of the tank, and not the water, so it displaces its volume, not its weight. Thus rocks weigh the same in the tank as they do outside of it.
6.
Back to pressure. Bernoulli’s principle stats that the faster a fluid moves, the lower its pressure. This is the basis for the operation of a python. They water flowing out of the faucet is moving and thus at a lower pressure than the air in the hose. Since pressure tries to equalize, the air in the hose lowers as air runs out of the python outlet with the water. This causes the water to be “sucked” out of the tank. Saying it sucks isn’t quite right. When you suck on a straw you don’t really suck, you cause the pressure in the atmosphere to push the liquid down and it goes up through the straw since the pressure is lower. Here is a picture to help show this.
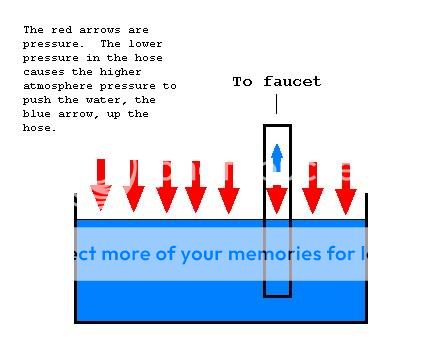
Bernoulli’s equation is:
P1 + (½ x D x V1^2) + DxGxH1 = P2 + (½ x D x V2^2) + DxGxH2. P is atmospheric pressure, D is density of the fluid, V is the velocity of the fluid, G is the rate of gravity, and H is the depth of the
You can use this to find a flow rate based on pressure. The problem with finding this using a python is that I don’t know what the water pressure coming out of your faucet is (and you can vary it). However, with a regular gravel vac, you can calculate this quite easily. The side with the 1’s is going to be the hose output, and the side with the 2’s is going to be the tank. Since the tank pressure is basically the same as the atmospheric pressure the P’s cancel. The tank water is not moving (for practical purposes), so (½ x D x V2^2)=0. We will let the hose output be zero, so DxGxH1 = 0. This leaves us with:
½ x D x V1^2= D x G x H2
H2 is the height from the hose outlet to the top of the water in the tank. The D’s cancel and multiplying both sides by 2 we get.
V1^2=2xGxH2 or V1=sqrt(2xG x H) sqrt=square root.
Lets just say that the height is about 1.5 feet from the top of the tank water, to the hose out put. Gravity is 32 feet/sec/sec, so
V1= Sqrt ( 2x32x 1.5) =9.8 feet/ sec = 6.7 mph
If the radius of the hose is r= 1/8 of an inch, or 1/96 of a foot then the area of its opening is A=Pi x r^2 = 3.14 x (1/48)^2=.00034 square feet
The flow rate in volume is then, the speed times the area of the opening.
VxA= 8.9 f/s x .00034 square feet = .003 cubic feet per second. Since 1 gallon is .133 cubic feet, then (.003 cf/s) / (.133 cf/gal)= .023 gal/sec.
To get sec/gal, take the inverse of .023, which is 1/.023= 44 sec/gal.
To do a 50% water change in a ten gallon, it takes about 220 seconds, or 3 minutes 40 seconds(5x44). I haven’t timed it or measured the actual height from the hose opening to the water surface, but it does sound about right.
Power filters and power heads use an impeller to push the water away from the opening of the inlet tube. The vacuum that is left causes water to be pulled up into the filter. This is the basic operation of these systems. I would like to elaborate more on it, but this is a more specific application and a hydraulic engineer would probably be able to give some more specific information than I can right now.
7.
OK time for a change of subject. Let’s talk about something shocking! Electricity.
First the basics, some common terms.
Voltage: This is the measure of a difference in charge. If you read 10 volts on a meter, it means that one side is 10 volts more than the other side, it doesn’t measure zero volts. We usually take ground to be zero since it is big and convenient.
Current: This is the flow of charge per second
Wattage: This is a measure of electrical power, or work per second.
I won’t get into ohm’s law here, since it really isn’t important to the discussions. But to calculate power, for most applications, you multiply voltage times current.
There are grounding probes out there for fish tanks. The idea is that if the tank has a net charge compared to you, and you stick your hand in there, you get shocked. This isn’t normally an issue unless you have a heater or filter leaking current, which usually doesn’t happen. The grounding probe simply allows any charge in the tank to equalize with ground voltage.
One of the common wonderings on this site is how much it costs to run their aquarium. To find this simply look up the power ratings, or calculate it, and add them together. NOTE, if lights are on for 12 hours and the heater is only on half the time, then you need to take that into account. I am assuming the filter and air pump are on 24/7. This isn’t technically the correct way to look at it. It should be that they the time they are on is halved, but the math works out the same.
For example:
150 Watt heater on half the time is 75 watts
40 Watt’s of light on 12 hours a day is 20W.
8 Watt fliter
3 Watt air pump
Add these together to get 106 Watts. Electricity is charged at in kilo-watt hours, so take the watt’s times days in a month times 24 hours times the cost of your electricity divided by 1000. This is your monthly cost. Eg.
106x30x24x.085/1000 = $6.49 per month.
8.
Oh no, the fish are getting cold! Its winter and the power has been out all day!
So how cold does the aquarium actually get? Well as many have probably heard, larger tanks have more stable water. This is true with temperature too. Since heat is only lost at the surface, larger tanks take longer too cool. Compare a pot of hot water with a cup of hot water.
The world of thermodynamics can get very odd and confusing fairly quickly, but in this case it shouldn’t be too complicated. I won’t get into the atomic theory of matter or kinetic theory, as this my over complicate things.
The first thing that is needed to know is the zeroth law of thermodynamics. It states that if two things with different temperatures come in contact with each other, they will equalize in temperature. This sounds too obvious to state, but it was needed to explain more complex systems. (this is why it is the zeroth law, the first law was already stated, and this is needed before the first law, for the first law to make sense.) The first law of thermodynamics is U= Q-W which seems simple but in practice, its very confusing remembering how to use the values, but I digress. The first law isn’t necessary for this article. Since a tank is usually at a higher temperature than the air around it, it looses heat to the air through the glass, and through the surface to the air. To actually find how much heat a tank actually looses is quite difficult because of all of the variable involved, and the different ways that it looses heat, but we can make a rough approximation of this.
We need to learn about specific heat and conduction. Specific heat is the amount of heat needed to raise something one degree. It is given by the equation:
Q=mcdT , Where Q is the heat, m is the mass of the object, dT is the change in temperature, and c is the specific heat constant, and is a characteristic of the material.
For conduction, we have the change in heat, dQ/dt=kA(T1-T2)/L. Where dQ/dt is the rate of change in heat, in our cause it will just be per second to keep things simple. k is the thermal conductivity constant and is a property of the material. T1-T2 is the difference in temperature on each side of the object. L is the length of the object
First we will need to find the amount of heat lost to the surface of the aquarium. This is made more difficult by the fact that the aquarium is covered. There are different materials, and some openings to let some air in and out. The easiest way is to assume that the top is either open, covered completely by glass, or completely covered by wood or plastic.
Too keep this example as easy as possible, I’ll assume that all sides of a rectangular aquarium are completely covered by glass that is .0065m (1/4 inch) thick, which will be L. First we need to find the total surface area of the glass in the tank. I’ll figure this out for a 29 gallon tank. Remember the dimensions are 30x12x18 inches or 76.2cm x 30.5cm x 45.7cm
The front and the back panes of glass are 2 x 76.2 x 45.7 = 6965 square cm.
The side panes are 2 x 30.5 x 45.7 =2788 square cm.
The top and bottom are 2 x 76.2 x 30.5=4648 square cm.
Adding these together gives us 14400 square cm or 1.44 square meters of surface area, which is A.
We are going to further simplify this by assuming that the room temperature is 20 degrees C (68 degrees f) and stays steady, and that the tanks temperature was at 25.5 degrees C (78 degrees f) when the power goes out (or when the heater fails off.) The k for glass is .84 J/(smC) [joules / (second meter degree C)] (joule is a unit of energy).
dQ/dt = kA(T1-T2)/L = .84x 1.44(25.5-20)/.0065=1023J/S
Notice how this doesn’t depend on the fact that water is on one side of the glass and air is on the other. This is because of the zeroth law. Regardless of what the materials are, they always try to become in equilibrium temperature with each other.
Using specific heat we can find how much heat must be lost to change the temperature of the tank to the temperature of the room. The mass of the water in the tank is 106 kg and the specific heat of water is c=4186, and dT is 25.5-20=5.5 C
Q=mcdT =106 x 4186 x 5.5 = 2440000J
2440000J / 1023J/S = 2385.5 seconds, or about 40 minutes to cool from 78 degrees to 68 degrees. This is a very very very simplified calculation, and is not very accurate. It doesn’t take into account a lot of factors. If your tank is sitting on a wooden stand with a solid wooden top it will loose much less heat through the bottom. Additionally, if your hood is wood, it will reduce heat loss even more. The gravel in your tank has a lower specific heat and will cool more easily than water. Everything radiates heat as well, but it is so small for water that it was neglected. I’ll explain more about this when I talk about light. There are just too many factors to get a completely accurate calculation here, but I would be willing to bet that if you were to try this with a tank with nothing but water in it and glass on all sides, it would be somewhat close to what actually happens. I don’t have a spare tank to try it on so I can’t confirm its accuracy by experiment.
9.
All about Light:
I could write for hours about light, its one of the most important topics in physics. Everything that you might hear that sounds difficult (quantum physics, atomic physics, nuclear physics ect.) are all related to light. I won’t get into all of that since it doesn’t directly relate to the aquarium.
Light is basically electro-magnetic radiation. It is the same thing as radio waves, micro waves, x rays, gamma rays ect… Here are some common parts of the E-M spectrum listed by frequency
60 Hz, wall frequency (in the US)
100-10MHz Radio waves
10MHz-1000GHz Micro waves
100GHz-40000GHz infrared light (there is over lap with micro waves)
40000GHz-75000GHz visible light
75000GHz-1millon GHz Ultra violet light
1million GHz- 100 million GHz X-rays
Greater than 100 million GHz Gamma rays
We are obviously interested in the visible spectrum, which is usually referred to as wave lengths, since it is this, and not frequency that determines color. The wave lengths of visible light range from 400 nm (violet) to 750 nm (red).
Where does light come from? This is both a difficult and easy question to answer. Light comes from electrons moving from a higher energy state to a lower energy state. Because of the law of conservation of energy, this energy has to go somewhere. It leaves as electromagnetic radiation. Depending on the circumstances, this is sometimes in the form of visible light. Light from the sun comes from two sources, nuclear fusion, and black body radiation. Nuclear fusion is the process of atoms fusing with each other to make heavier atoms. This results in a large change of energy from high levels to low levels, and thus releases a LOT of energy. Black body radiation is the principle that all objects give off some form of radiation. Calling it black body refers to the fact that black things are the “ideal” radiators, while white and shiny things do not radiate very much. (This is why it wasn’t taken into account for a cooling fish tank. Water isn’t very black, and the effect is minimal.)
The spectrum of light we get from the sun is almost that of an Ideal black body at 5800 degrees K. When you see people say that a 6500K light is best for planted tanks, this is why. The spectrum of light given off by the tube, is what would be given off by an ideal black body at that temperature. The light from the bulb is determined by the chemical coating inside the tube, so the output isn’t an exact duplicate of black body radiation. Light usage by plants peaks between 400-425 nm in the blue area, and 625-650 nm in the red range. Most of the other parts of the spectrum are of little use to plants.
Actinic lights (8000-10000K) have very little red light, which is the most important color for plants. They are used in reef tanks. Blue light has more energy than red light, so it penetrates deeper into the water. This is why the ocean often looks blue. It is also why its important. Since blue light is what’s available, coral and algae’s have adapted to use the blue light.
Light is measured in lumens, or lux (lumens, per area). Most lighting is fluorescent. Since it is fairly consistent, people usually use a watts per gallon rule. This rule breaks down when you use different sources of light. Fluorescent is used, because it is efficient, and fairly easy to control what color are produced. Incandescent isn’t very efficient, and gives of more heat than light. It also doesn’t give off a good spectrum for growing plants. Metal halide lamps and mercury vapor lamps don’t produce the best spectrums of light, but they put out so much light, that it makes up for this and are good for deep tanks. Be careful with these, they get hot and the oils from your fingers on the glass can cause them to explode!
10.
Honey Look, The fish are refracting!!
Its not a disease, its bending light. When light goes though something of a different density, it changes speed. This change of speed causes it to bend, creating the appearance of things looking closer than they are in an aquarium. This is best illustrated with a picture
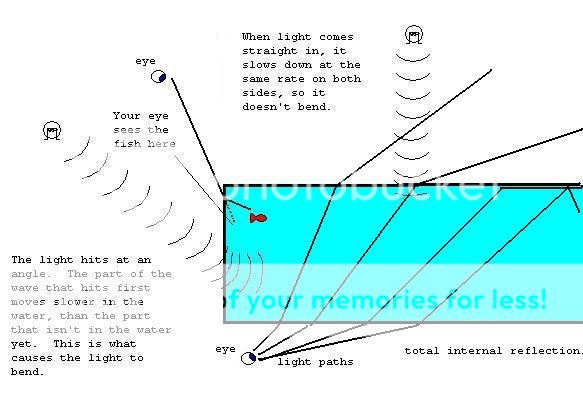
The human brain assumes that light comes in at a straight line. This is the tank looks smaller from the out side, or why you can look at a tank from the corner of it, and see the same thing through both the front pane of glass and the side. Another common phenomena of this is total internal reflection. When looking from inside the water looking out, the light bends the same way and gives a mirror effect. When you get to the proper angle, the light runs along the glass, and past that point, it reflects back off of the glass.
Not technically physics but relevant math non-the less.
Ever want to know what your normal level of nitrates will be? Here is how to do it. After a water change measure your nitrate level. The time of your next water change, measure the nitrates again, the difference is A. If you do a 50% water change, you remove 50% of your nitrates. Here is the equation.
dN/dt = -.50N + A Where N is your total nitrates.
Basically this equation says that your change in nitrates increase at rate A per interval between water changes, and also decreases at your percent times the total nitrates. When the rate of change is zero, your nitrates stay the same, so this is the equilibrium point. Set the equation to zero, and solve for N. Here is an example. My tank produces 10 nitrates per week, and I do 40 percent water changes once a week, so my equation is
0 = -.40 N +10
.40N = 10
N=25
This will my usual nitrate level when I do every water change. It is a simple model, and may not always be accurate, since aquariums are not constant, and are always changing. It is fairly close though since the aquarium shouldn’t change too much.
Well, there you have it. I hope I was able to hit the most relevant points. I am sure there were things that I forgot to talk about. If anyone has ideas for topics that I can add, please feel free to suggest them. If anyone has any further questions, again please ask. If you have found any errors, let me know so I can fix them.
Joephys.
1. Volume
2. Weight
3. Pressure
4. Stress on glass
5. Buoyancy
6. More about pressure, including gravel vac’s and pythons.
7. A little bit about electricity. (power usage and cost calculations)
8. How fast the tank cools.
9. More than you ever wanted to know about light
10. Those whacky refracting fishies
Ok, enough of that, time for the relevant stuff.
1.
Just how much water is in my tank?
This question is asked a lot, so here it is.
For a rectangle tank, you need to measure the length (L), width (W) and height (H) of the tank, then multiply them together. Volume (V)=LxWxH
Here are some examples for common tanks.
10 gallon:
L= 20 in V=20x10x12
W= 10 in V=2400 cu.in.
H= 12 in
29 gallon:
L=30 in V=30x12x18
W=12 in V=6480 cu.in
H= 18 in
55 gallon:
L=48 V= 48x13x20
W=13 V=12480 cu.in.
H=20
For some other odd shaped tanks:
Hex (all sides same length):
Find the length of a side (L)
Find the distance from the center of one flat side, to the opposite flat side (W).
Find the height of the tank (H).
V = 3xLxWxH
Cylinder:
Find the distance across the tank and divide by 2 (R).
Find the height of the tank (H).
V= 3.14 x R^2 x H (Note: R^2=R squared, or RxR)
Bow fronts can be difficult to measure. If the bow is perfectly circular or parabolic then it maybe possible to calculate the volume, but it is a lot of work and more easily done in different coordinates. I don’t want to get into that since I said that I would keep the math on the easier side.
For volume in gallons you multiply the volume in cubic what ever (inches in the examples) by a water volume constant (B). For inches B= .0043 For feet B = 7.5, thus, gallons=VxB
Examples:
10 gallons:
G= 2400x .0043= 10.3 gal
29 gallons:
G= 6480x .0043=27.9 gal
55 gallons:
G=12480x .0043= 53.7 gal.
As you can see, the advertised volumes are not the actual volumes of the tanks.
2.
Weight:
Calculating the actual weight of the aquarium can be quite difficult. You need the weight of the empty tank, all the decorations and gravel in the tank, and the amount of water in the tank. Water weighs 8.5 lbs per gallon, so for the average tank, you can assume about 10-12 lbs per gallons depending on what you have in it. Simply multiply the volume of the tank in gallons by 10 (in these examples) to get an approximate weight.
10 gallons:
W= 10x10 =100 lbs
29 gallons:
W= 29x10 = 290 lbs
55 gallons:
W = 55x10 = 550 lbs
As you can see, some tanks can get very heavy very fast. The 55 gallon weighs over a quarter of a ton!
3.
Oh the pressure!!! Just what is the water pressure down there? Just how deep can your air pump or CO2 go?
Well, pressure basically the weight of all the air in the atmosphere air and the weight of the water per one unit of area, usually per square inch. Normal atmospheric pressure is 14.7 pounds per square inch (psi). This means that if you draw a square on the ground one inch on each side, all of the air above it, from the ground to the edge of the atmosphere way up there weighs 14.7 lbs. Most measurements of pressure are relative to this. If your pump is rated at 1 psi, it is putting out 15.7 psi, but because the back pressure is 14.7, the net effect is 1 psi. All of our measurements are going to be relative to the atmospheric pressure.
Water pressure depends only on depth. To find it is simple, just multiply the density of water times its depth. The density of water (d) is .036 pounds per cubic inch (at sea level).
P= dxh
Examples:
10 gallons:
P= .036x 12 = .43 psi
29 gallons:
P= .036x 18 = .65 psi
55 gallons:
P= .036x 20= .72 psi.
If you have a small air pump rated at 1 psi, then it will just barely work in a 55 gallon tank, and its effective pressure out is only about .28 psi.
4.
Speaking of pressure, how strong is that silicone anyway?
Here is one place that things start to get a little more tricky, as this requires calculus. (OH NOW HIT THE BACK BUTTON NOW!!!!) No, no, no, don’t worry, its ok, you don’t need the calculus to figure it out in your tank, it’s just required to find the equation.
One think you need to know about pressure is that it works in “pushes” in every direction equally, so if the pressure is 10 psi, that means that on the sides of the tank, there are 10 psi.
To find the force on the side of the tank you simply need to multiply the area of the glass by the pressure. But wait, its not that simple, the pressure changes with depth. This is why the calculus is needed. If you under stand it, its included in the next paragraph. If not, then just ignore it and use the equation in the last line.
Note: I cannot make an integral sign, so I’ll use int(..) instead.
F = int( dxWxh dh) dh refers to the variable being integrated with respect to, basically.
F = ½ xdxWxh^2
To find the force on the side of the tank, just plug the numbers into the above formula.
Example (front or back walls):
10 gallons:
F= ½ x .036x20x12^2
F= 52 lbs.
29 gallons:
F= ½ x.036x30x18^2
F=175 lbs.
55 gallons:
F= ½ x.036x48x20^2
F= 346 lbs.
As you can see, there is a lot of force on the sides of a tank. Kind of makes you want to ensure your center brace is there huh? Notices that if you add up the forces on the front, back and side walls, it is more than the weight of the tank!!!
5.
While we are still on the topic of water, lets talk about water displacement. I remember a post once where someone asked if, since water displaces the weight of an object, does that mean that rocks weigh less? Well, the short answer is no.
Archimedes principle states that an object displaces its weight in water if it is floating (and only floating). Basically if something that is 10 lbs is floating, then it displaces 10 lbs of water. The volume of the water displaced is the same volume of the amount of the object under water. That is why ice is mostly under water when it floats (its just slightly lighter than water). When an object doesn’t float, its weight is being supported by the bottom of the tank, and not the water, so it displaces its volume, not its weight. Thus rocks weigh the same in the tank as they do outside of it.
6.
Back to pressure. Bernoulli’s principle stats that the faster a fluid moves, the lower its pressure. This is the basis for the operation of a python. They water flowing out of the faucet is moving and thus at a lower pressure than the air in the hose. Since pressure tries to equalize, the air in the hose lowers as air runs out of the python outlet with the water. This causes the water to be “sucked” out of the tank. Saying it sucks isn’t quite right. When you suck on a straw you don’t really suck, you cause the pressure in the atmosphere to push the liquid down and it goes up through the straw since the pressure is lower. Here is a picture to help show this.

Bernoulli’s equation is:
P1 + (½ x D x V1^2) + DxGxH1 = P2 + (½ x D x V2^2) + DxGxH2. P is atmospheric pressure, D is density of the fluid, V is the velocity of the fluid, G is the rate of gravity, and H is the depth of the
You can use this to find a flow rate based on pressure. The problem with finding this using a python is that I don’t know what the water pressure coming out of your faucet is (and you can vary it). However, with a regular gravel vac, you can calculate this quite easily. The side with the 1’s is going to be the hose output, and the side with the 2’s is going to be the tank. Since the tank pressure is basically the same as the atmospheric pressure the P’s cancel. The tank water is not moving (for practical purposes), so (½ x D x V2^2)=0. We will let the hose output be zero, so DxGxH1 = 0. This leaves us with:
½ x D x V1^2= D x G x H2
H2 is the height from the hose outlet to the top of the water in the tank. The D’s cancel and multiplying both sides by 2 we get.
V1^2=2xGxH2 or V1=sqrt(2xG x H) sqrt=square root.
Lets just say that the height is about 1.5 feet from the top of the tank water, to the hose out put. Gravity is 32 feet/sec/sec, so
V1= Sqrt ( 2x32x 1.5) =9.8 feet/ sec = 6.7 mph
If the radius of the hose is r= 1/8 of an inch, or 1/96 of a foot then the area of its opening is A=Pi x r^2 = 3.14 x (1/48)^2=.00034 square feet
The flow rate in volume is then, the speed times the area of the opening.
VxA= 8.9 f/s x .00034 square feet = .003 cubic feet per second. Since 1 gallon is .133 cubic feet, then (.003 cf/s) / (.133 cf/gal)= .023 gal/sec.
To get sec/gal, take the inverse of .023, which is 1/.023= 44 sec/gal.
To do a 50% water change in a ten gallon, it takes about 220 seconds, or 3 minutes 40 seconds(5x44). I haven’t timed it or measured the actual height from the hose opening to the water surface, but it does sound about right.
Power filters and power heads use an impeller to push the water away from the opening of the inlet tube. The vacuum that is left causes water to be pulled up into the filter. This is the basic operation of these systems. I would like to elaborate more on it, but this is a more specific application and a hydraulic engineer would probably be able to give some more specific information than I can right now.
7.
OK time for a change of subject. Let’s talk about something shocking! Electricity.
First the basics, some common terms.
Voltage: This is the measure of a difference in charge. If you read 10 volts on a meter, it means that one side is 10 volts more than the other side, it doesn’t measure zero volts. We usually take ground to be zero since it is big and convenient.
Current: This is the flow of charge per second
Wattage: This is a measure of electrical power, or work per second.
I won’t get into ohm’s law here, since it really isn’t important to the discussions. But to calculate power, for most applications, you multiply voltage times current.
There are grounding probes out there for fish tanks. The idea is that if the tank has a net charge compared to you, and you stick your hand in there, you get shocked. This isn’t normally an issue unless you have a heater or filter leaking current, which usually doesn’t happen. The grounding probe simply allows any charge in the tank to equalize with ground voltage.
One of the common wonderings on this site is how much it costs to run their aquarium. To find this simply look up the power ratings, or calculate it, and add them together. NOTE, if lights are on for 12 hours and the heater is only on half the time, then you need to take that into account. I am assuming the filter and air pump are on 24/7. This isn’t technically the correct way to look at it. It should be that they the time they are on is halved, but the math works out the same.
For example:
150 Watt heater on half the time is 75 watts
40 Watt’s of light on 12 hours a day is 20W.
8 Watt fliter
3 Watt air pump
Add these together to get 106 Watts. Electricity is charged at in kilo-watt hours, so take the watt’s times days in a month times 24 hours times the cost of your electricity divided by 1000. This is your monthly cost. Eg.
106x30x24x.085/1000 = $6.49 per month.
8.
Oh no, the fish are getting cold! Its winter and the power has been out all day!
So how cold does the aquarium actually get? Well as many have probably heard, larger tanks have more stable water. This is true with temperature too. Since heat is only lost at the surface, larger tanks take longer too cool. Compare a pot of hot water with a cup of hot water.
The world of thermodynamics can get very odd and confusing fairly quickly, but in this case it shouldn’t be too complicated. I won’t get into the atomic theory of matter or kinetic theory, as this my over complicate things.
The first thing that is needed to know is the zeroth law of thermodynamics. It states that if two things with different temperatures come in contact with each other, they will equalize in temperature. This sounds too obvious to state, but it was needed to explain more complex systems. (this is why it is the zeroth law, the first law was already stated, and this is needed before the first law, for the first law to make sense.) The first law of thermodynamics is U= Q-W which seems simple but in practice, its very confusing remembering how to use the values, but I digress. The first law isn’t necessary for this article. Since a tank is usually at a higher temperature than the air around it, it looses heat to the air through the glass, and through the surface to the air. To actually find how much heat a tank actually looses is quite difficult because of all of the variable involved, and the different ways that it looses heat, but we can make a rough approximation of this.
We need to learn about specific heat and conduction. Specific heat is the amount of heat needed to raise something one degree. It is given by the equation:
Q=mcdT , Where Q is the heat, m is the mass of the object, dT is the change in temperature, and c is the specific heat constant, and is a characteristic of the material.
For conduction, we have the change in heat, dQ/dt=kA(T1-T2)/L. Where dQ/dt is the rate of change in heat, in our cause it will just be per second to keep things simple. k is the thermal conductivity constant and is a property of the material. T1-T2 is the difference in temperature on each side of the object. L is the length of the object
First we will need to find the amount of heat lost to the surface of the aquarium. This is made more difficult by the fact that the aquarium is covered. There are different materials, and some openings to let some air in and out. The easiest way is to assume that the top is either open, covered completely by glass, or completely covered by wood or plastic.
Too keep this example as easy as possible, I’ll assume that all sides of a rectangular aquarium are completely covered by glass that is .0065m (1/4 inch) thick, which will be L. First we need to find the total surface area of the glass in the tank. I’ll figure this out for a 29 gallon tank. Remember the dimensions are 30x12x18 inches or 76.2cm x 30.5cm x 45.7cm
The front and the back panes of glass are 2 x 76.2 x 45.7 = 6965 square cm.
The side panes are 2 x 30.5 x 45.7 =2788 square cm.
The top and bottom are 2 x 76.2 x 30.5=4648 square cm.
Adding these together gives us 14400 square cm or 1.44 square meters of surface area, which is A.
We are going to further simplify this by assuming that the room temperature is 20 degrees C (68 degrees f) and stays steady, and that the tanks temperature was at 25.5 degrees C (78 degrees f) when the power goes out (or when the heater fails off.) The k for glass is .84 J/(smC) [joules / (second meter degree C)] (joule is a unit of energy).
dQ/dt = kA(T1-T2)/L = .84x 1.44(25.5-20)/.0065=1023J/S
Notice how this doesn’t depend on the fact that water is on one side of the glass and air is on the other. This is because of the zeroth law. Regardless of what the materials are, they always try to become in equilibrium temperature with each other.
Using specific heat we can find how much heat must be lost to change the temperature of the tank to the temperature of the room. The mass of the water in the tank is 106 kg and the specific heat of water is c=4186, and dT is 25.5-20=5.5 C
Q=mcdT =106 x 4186 x 5.5 = 2440000J
2440000J / 1023J/S = 2385.5 seconds, or about 40 minutes to cool from 78 degrees to 68 degrees. This is a very very very simplified calculation, and is not very accurate. It doesn’t take into account a lot of factors. If your tank is sitting on a wooden stand with a solid wooden top it will loose much less heat through the bottom. Additionally, if your hood is wood, it will reduce heat loss even more. The gravel in your tank has a lower specific heat and will cool more easily than water. Everything radiates heat as well, but it is so small for water that it was neglected. I’ll explain more about this when I talk about light. There are just too many factors to get a completely accurate calculation here, but I would be willing to bet that if you were to try this with a tank with nothing but water in it and glass on all sides, it would be somewhat close to what actually happens. I don’t have a spare tank to try it on so I can’t confirm its accuracy by experiment.
9.
All about Light:
I could write for hours about light, its one of the most important topics in physics. Everything that you might hear that sounds difficult (quantum physics, atomic physics, nuclear physics ect.) are all related to light. I won’t get into all of that since it doesn’t directly relate to the aquarium.
Light is basically electro-magnetic radiation. It is the same thing as radio waves, micro waves, x rays, gamma rays ect… Here are some common parts of the E-M spectrum listed by frequency
60 Hz, wall frequency (in the US)
100-10MHz Radio waves
10MHz-1000GHz Micro waves
100GHz-40000GHz infrared light (there is over lap with micro waves)
40000GHz-75000GHz visible light
75000GHz-1millon GHz Ultra violet light
1million GHz- 100 million GHz X-rays
Greater than 100 million GHz Gamma rays
We are obviously interested in the visible spectrum, which is usually referred to as wave lengths, since it is this, and not frequency that determines color. The wave lengths of visible light range from 400 nm (violet) to 750 nm (red).
Where does light come from? This is both a difficult and easy question to answer. Light comes from electrons moving from a higher energy state to a lower energy state. Because of the law of conservation of energy, this energy has to go somewhere. It leaves as electromagnetic radiation. Depending on the circumstances, this is sometimes in the form of visible light. Light from the sun comes from two sources, nuclear fusion, and black body radiation. Nuclear fusion is the process of atoms fusing with each other to make heavier atoms. This results in a large change of energy from high levels to low levels, and thus releases a LOT of energy. Black body radiation is the principle that all objects give off some form of radiation. Calling it black body refers to the fact that black things are the “ideal” radiators, while white and shiny things do not radiate very much. (This is why it wasn’t taken into account for a cooling fish tank. Water isn’t very black, and the effect is minimal.)
The spectrum of light we get from the sun is almost that of an Ideal black body at 5800 degrees K. When you see people say that a 6500K light is best for planted tanks, this is why. The spectrum of light given off by the tube, is what would be given off by an ideal black body at that temperature. The light from the bulb is determined by the chemical coating inside the tube, so the output isn’t an exact duplicate of black body radiation. Light usage by plants peaks between 400-425 nm in the blue area, and 625-650 nm in the red range. Most of the other parts of the spectrum are of little use to plants.
Actinic lights (8000-10000K) have very little red light, which is the most important color for plants. They are used in reef tanks. Blue light has more energy than red light, so it penetrates deeper into the water. This is why the ocean often looks blue. It is also why its important. Since blue light is what’s available, coral and algae’s have adapted to use the blue light.
Light is measured in lumens, or lux (lumens, per area). Most lighting is fluorescent. Since it is fairly consistent, people usually use a watts per gallon rule. This rule breaks down when you use different sources of light. Fluorescent is used, because it is efficient, and fairly easy to control what color are produced. Incandescent isn’t very efficient, and gives of more heat than light. It also doesn’t give off a good spectrum for growing plants. Metal halide lamps and mercury vapor lamps don’t produce the best spectrums of light, but they put out so much light, that it makes up for this and are good for deep tanks. Be careful with these, they get hot and the oils from your fingers on the glass can cause them to explode!
10.
Honey Look, The fish are refracting!!
Its not a disease, its bending light. When light goes though something of a different density, it changes speed. This change of speed causes it to bend, creating the appearance of things looking closer than they are in an aquarium. This is best illustrated with a picture

The human brain assumes that light comes in at a straight line. This is the tank looks smaller from the out side, or why you can look at a tank from the corner of it, and see the same thing through both the front pane of glass and the side. Another common phenomena of this is total internal reflection. When looking from inside the water looking out, the light bends the same way and gives a mirror effect. When you get to the proper angle, the light runs along the glass, and past that point, it reflects back off of the glass.
Not technically physics but relevant math non-the less.
Ever want to know what your normal level of nitrates will be? Here is how to do it. After a water change measure your nitrate level. The time of your next water change, measure the nitrates again, the difference is A. If you do a 50% water change, you remove 50% of your nitrates. Here is the equation.
dN/dt = -.50N + A Where N is your total nitrates.
Basically this equation says that your change in nitrates increase at rate A per interval between water changes, and also decreases at your percent times the total nitrates. When the rate of change is zero, your nitrates stay the same, so this is the equilibrium point. Set the equation to zero, and solve for N. Here is an example. My tank produces 10 nitrates per week, and I do 40 percent water changes once a week, so my equation is
0 = -.40 N +10
.40N = 10
N=25
This will my usual nitrate level when I do every water change. It is a simple model, and may not always be accurate, since aquariums are not constant, and are always changing. It is fairly close though since the aquarium shouldn’t change too much.
Well, there you have it. I hope I was able to hit the most relevant points. I am sure there were things that I forgot to talk about. If anyone has ideas for topics that I can add, please feel free to suggest them. If anyone has any further questions, again please ask. If you have found any errors, let me know so I can fix them.
Joephys.


